How To Find Log Without Using Log Table And Calculator
 | Math Skills Review Logarithms |
Two kinds of logarithms are ofttimes used in chemical science: common (or Briggian) logarithms and natural (or Napierian) logarithms. The power to which a base of 10 must be raised to obtain a number is chosen the common logarithm (log) of the number. The power to which the base due east (e = two.718281828.......) must be raised to obtain a number is called the natural logarithm (ln) of the number.
In simpler terms, my 8th grade math teacher ever told me: LOGS ARE EXPONENTS!! What did she mean by that?
- Using logx ("log to the base 10"):
log10100 = ii is equivalent to 102 = 100
where x is the base, 2 is the logarithm (i.e., the exponent or power) and 100 is the number. - Using natural logs (loge or ln):
Conveying all numbers to 5 significant figures,
ln thirty = 3.4012 is equivalent to e3.4012 = 30 or two.71833.4012 = xxx - Many equations used in chemistry were derived using calculus, and these often involved natural logarithms. The relationship between ln x and log x is:
ln x = two.303 log x Why 2.303? Allow'due south utilise ten = x and observe out for ourselves.
Rearranging, we accept (ln 10)/(log ten) = number.
We tin can easily summate that ln 10 = 2.302585093... or 2.303 and log 10 = one.
So, the number has to be 2.303. Voila! - Historical note: Before calculators, we used slide rules (a tool based on logarithms) to do calculations requiring iii significant figures. If we needed more three signficant figures, we pulled out our lengthy logarithm tables. Anyway, enough history......
The balance of this mini-presentation will concentrate on logarithms to the base 10 (or logs). One use of logs in chemical science involves pH, where pH = -log10 of the hydrogen ion concentration.
FINDING LOGARITHMS
Here are some simple examples of logs.
| Number | Exponential Expression | Logarithm |
|---|---|---|
| 1000 | 103 | iii |
| 100 | 10two | two |
| 10 | ten1 | 1 |
| i | 100 | 0 |
| 1/x = 0.1 | x -1 | -ane |
| 1/100 = 0.01 | 10 -2 | -2 |
| 1/m = 0.001 | ten -3 | -3 |
To find the logarithm of a number other than a ability of 10, y'all demand to utilise your scientific reckoner or pull out a logarithm table (if they withal exist). On most calculators, you lot obtain the log (or ln) of a number past
- entering the number, then
- pressing the log (or ln) button.
- Case 1: log v.43 ten 1010 = ten.73479983...... (way too many significant figures)
- Example 2: log two.seven x x -viii = -7.568636236...... (too many sig. figs.)
So, permit'south wait at the logarithm more than closely and figure out how to determine the correct number of significant figures it should accept.
For any log, the number to the left of the decimal point is chosen the feature, and the number to the right of the decimal bespeak is called the mantissa. The characteristic only locates the decimal point of the number, then it is usually not included when determining the number of significant figures. The mantissa has as many significant figures every bit the number whose log was institute. So in the in a higher place examples:
- Example ane: log five.43 x 10ten = 10.735
The number has iii pregnant figures, just its log ends upward with v significant figures, since the mantissa has three and the characteristic has 2. - Instance 2: log ii.seven x 10 -viii = -vii.57
The number has 2 significant figures, but its log ends upward with 3 significant figures.
Natural logarithms piece of work in the same way:
- Example iii: ln iii.95 x xhalf dozen = xv.18922614... = xv.189
Application to pH bug:
- Example four: What is the pH of an aqueous solution when the concentration of hydrogen ion is 5.0 x 10 -4 M?
pH = -log [H+] = -log (5.0 ten 10 -4) = - (-3.30) = 3.30
FINDING ANTILOGARITHMS (also called Inverse Logarithm)
Sometimes we know the logarithm (or ln) of a number and must work backwards to find the number itself. This is called finding the antilogarithm or inverse logarithm of the number. To do this using most uncomplicated scientific calculators,
- enter the number,
- press the inverse (inv) or shift button, and so
- press the log (or ln) push. It might also exist labeled the 10ten (or due eastten) push.
- Instance 5: log x = 4.203; so, ten = inverse log of 4.203 = 15958.79147..... (likewise many significant figures)
There are three meaning figures in the mantissa of the log, so the number has 3 significant figures. The respond to the correct number of significant figures is one.60 x 104. - Instance 6: log x = -15.iii;
and then, x = inv log (-fifteen.3) = five.011872336... x x -16 = five x ten -xvi (one meaning figure)
Natural logarithms piece of work in the same way:
- Instance vii: ln x = 2.56; so, x = inv ln (two.56) = 12.93581732... = 13 (two sig. fig.)
Application to pH problems:
- Case eight: What is the concentration of the hydrogen ion concentration in an aqueous solution with pH = 13.22?
pH = -log [H+] = xiii.22
log [H+] = -thirteen.22
[H+] = inv log (-13.22)
[H+] = vi.0 10 x -14 M (two sig. fig.)
CALCULATIONS INVOLVING LOGARITHMS
Because logarithms are exponents, mathematical operations involving them follow the same rules as those for exponents.
| Common Logarithm | Natural Logarithm |
|---|---|
| log xy = log x + log y | ln xy = ln x + ln y |
| log x/y = log x - log y | ln 10/y = ln ten - ln y |
| log xy = y log 10 | ln teny = y ln x |
log 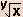 = log 101/y = (ane/y )log x = log 101/y = (ane/y )log x | ln 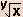 = ln teni/y =(ane/y)ln x = ln teni/y =(ane/y)ln x |
- Case 9: log five.0 ten 106 = log five.0 + log 10vi = 0.70 + 6 = 6.seventy
Hint: This is an piece of cake way to gauge the log of a number in scientific notation! - Instance 10: log (154/25) = log 154 - log 25 = 2.188 - ane.twoscore = 0.788 = 0.79 (2 sig. fig.)
- Example eleven: log (v.46 x ten -3)half-dozen = 6 log five.46 x x -3 = six x (-2.263) = -thirteen.58
- Example 12: log (iv.35)one/iv = 1/iv log four.35 = 0.160
QUIZ: Requite the right answer to the correct number of significant figures.
| Question 1 | log 23.0 = ? |
| Question 2 | What is the pH of an aqueous solution in which [H+] = two.7 x ten -three M? |
| Question three | Find x if log x = 10.23. |
| Question 4 | If the pH of an aqueous solution is 6.52, what is the concentration of the hydrogen ion? |
| Question v | log (1.two x xhalf-dozen)3 = ? |
Answers: (one) 1.362 (2) 2.57 (3) i.vii x 10x (4) iii.0 x 10 -vii M (v) 18.24
Option your next topic:
Source: https://www.chem.tamu.edu/class/fyp/mathrev/mr-log.html
Posted by: careydrife1958.blogspot.com


0 Response to "How To Find Log Without Using Log Table And Calculator"
Post a Comment