How To Find Initial Population With Exponential Growth
In that location is a substantial number of processes for which yous tin can utilize this exponential growth calculator. The general rule of thumb is that the exponential growth formula:
x(t) = ten0 * (1 + r/100)t
is used when there is a quantity with an initial value, ten0, that changes over time, t, with a constant rate of change, r. The exponential function appearing in the to a higher place formula has a base equal to ane + r/100.
Note that the exponential growth rate, r, tin be any positive number, but, this calculator also works as an exponential disuse estimator - where r also represents the rate of decay, which should be betwixt 0 & -100%. The reason for this is that y'all cannot accept a decline of more than 100% with regards to the initial quantity, equally it would upshot in a negative value.
The exponential growth equation is used in radiocarbon dating, PCR (you can discover why with our annealing temperature calculator) as well as in calculating compound interest. To learn more, please run across our compound interest estimator. For more examples of where y'all tin can utilize this formula, please check below.
How to calculate exponential growth
Consider the following problem: the population of a modest city at the starting time of 2019 was 10,000 people. It was noticed that the population of the metropolis grows at a steady rate of v% annually. What should y'all do to calculate the projected population size in the year 2030? From the given data, we can conclude the initial population value, x0, equals 10,000. Also, we have the growth rate of r = 5%.
Therefore, the exponential growth formula we should employ is:
x(t) = ten,000 * (1 + 0.05)t = ten,000 * 1.05t .
Here t is the number of years passed since 2019. In our example, for the year 2030, we should use t = eleven, since this is the deviation in the number of years betwixt 2030 and the initial twelvemonth 2019. Finally, we go:
x(eleven) = 10,000 * 1.0511 = 17,103.
Then, the projected number of inhabitants of our small city in the year 2030 is around 17,103.
If you want to dig a flake deeper into this particular formula, you can apply our exponential growth calculator to find out the projected number of inhabitants for each year, starting from 2019. This calculation results in the following tabular array, where nosotros round the results to the nearest integer:
| year | t | 10(t) |
|---|---|---|
| 2019 | 0 | 10,000 |
| 2020 | 1 | ten,500 |
| 2021 | 2 | 11,025 |
| 2022 | 3 | 11,576 |
| 2023 | 4 | 12,155 |
| 2024 | 5 | 12,763 |
| 2025 | 6 | xiii,401 |
| 2026 | seven | 14,071 |
| 2027 | 8 | xiv,775 |
| 2028 | 9 | fifteen,513 |
| 2029 | 10 | 16,289 |
| 2030 | 11 | 17,103 |
If you lot want to get an even better experience for the population growth, you may represent this information graphically, with the horizontal centrality being the time centrality and the vertical centrality representing the population value 10(t). The data from the table are all points lying on the continuous graph of the exponential growth function:
x(t) = x,000 * 1.05t .
Since the base of this exponential function is 1.05, and since it is greater than i, the exponential growth graph nosotros get is ascension. The main difference between this graph and the normal exponential office graph is that its y-intercept is not 1 but 10,000, which corresponds to the initial value ten0:
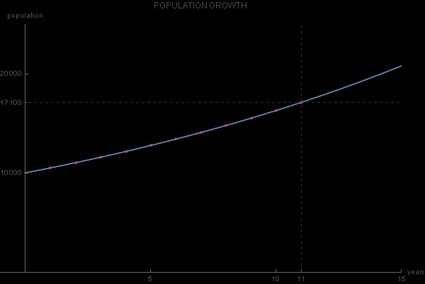
Example of exponential growth graph - population size
From this example, we tin see the possible limitations of the exponential growth model - information technology is unrealistic for the rate of growth to remain constant over time. Namely, it is difficult to await that the yearly rate of growth for the city's population would remain at 5% for a decade or more than.
In real life situations in that location are natural oscillations of the rate of growth which are not included in this model of exponential growth. A more than realistic model of population growth is the logistic growth model, which has the conveying chapters, a constant representing the population's natural growth limit.
How to notice the moment when the initial quantity reaches a given value
Continuing with our small city, the next question y'all may ask yourself is "when can we wait the population to reach some important value?" This is useful if you lot want to know when to adapt the city'due south urban planning for a larger population, and then the urban center council needs to know which yr they can await the city'southward population to have tripled in size from the original ten,000?
Here nosotros know how much is 10(t), but we don't know the value of t when this volition happen. Allow's do it footstep by stride:
-
Insert 10(t) = 30,000 into the formula:
xxx,000 = 10,000 * 1.05t -
After dividing both sides of the equation past 10,000, we get:
one.05t = 3. -
Have the logarithm to the base 1.05 of both sides of this equation:
t = logone.05 three. -
Apply the logarithm calculator to finally get:
t = 22.52.
And so, the answer to the quango's question is approximately 22 years after the initial year of 2019, and so in 2041:
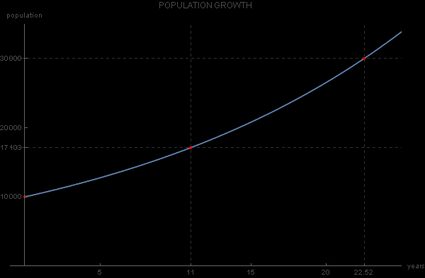
Example of exponential growth graph - population size
Can fourth dimension be negative?
You may have already noticed a problem with exponential growth and disuse, that it naturally treats time as only a positive value, then we are predicting a futurity quantity. All the same, this does not forbid us from using this formula with negative time values. This means that we describe the phenomenon of interest in the time before the initial ascertainment was made.
In the case of population growth, you lot may ask the question: what was the population of our modest city in the yr 2000, assuming the population growth rate was a constant 5%?
To solve this, y'all would employ t = -nineteen, since the year 2000 precedes the twelvemonth 2019 by xix years. The answer would therefore be
x(-xix) = x,000 * 1.05-nineteen = 3.957
inhabitants, as you can also come across on this graph:
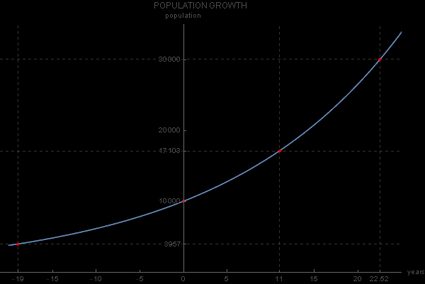
Example of exponential growth graph - population size
An alternative way of writing the exponential growth equation
For some applications, for instance when calculating the exponential decay of a radioactive substance, an culling way of writing downward the formula for exponential growth and decay is more productive:
x(t) = ten0 * eastk*t .
The coefficient k plays the role of the rate of growth, similarly as r does in the original exponential growth formula. Comparing the above equation with the original one, you tin come across that the relation between r and g is as follows:
1 + r/100 = ek , which means
r = 100 * (eastwardk - 1) and k = ln(1 + r/100).
Instance on how to employ the formula for exponential decay
Radioactive disuse is a well-known example of where the exponential decay formula is used. For a given initial quantity of radioactive substance, you may write downward the law which governs its decay over time. But, maybe a more than fun example is to measure how much java remains in your body at ten pm if you drank a cup of coffee with x0 = 95 mg of caffeine at apex.
Nosotros volition use the fact that the half-life of caffeine in the human body is approximately six hours. Half-life is defined as the time needed a given quantity to reduce to half of its initial value. So, in this example we have
x(6) = ane/ii * 95 mg = 47.5 mg.
Here, information technology volition exist easier to use the culling notation for the exponential growth formula:
x(t) = 95 * due eastk*t .
Hither is the footstep by step calculation:
-
Insert x(6)= 47.5 and t = half dozen into the equation:
47.v = 95 * e6k. -
This expression, after dividing both sides of the equation by 95 and applying the natural logarithm, gives:
6*k = ln 0.5. -
By using the natural logarithm calculator, we become:
yard = -0.1155. -
Therefore, the exponential decay formula in our case is:
x(t) = 95 * due east-0.1155 * t. -
Since ten pm is ten hours afterward than noon, we want to know the amount of caffeine at t = 10. Nosotros have:
x(ten) = 95 * e-0.1155 * 10 = 29.9305.
So, at 10 pm, the corporeality of caffeine remaining in your body will be approximately 30 mg.
What if there's no time at all?
Time tin be expressed in basically any appropriate units. For some problems, these volition be seconds, for others, years. Yous should cull the time unit in a fashion that corresponds to the nature of the observed procedure. For instance, if y'all want to understand the alter in the population of a city, you should choose years. On the other hand, if you're going to calculate the amount of coffee remaining in your trunk afterward you drank a loving cup of it, the appropriate time unit should be hours or possibly minutes.
Please note that t doesn't really have to exist considered equally time just. In some cases, the variable which measures the rate of alter can be unlike than time. For example, when studying the way that atmospheric pressure changes with altitude, the variable measuring this change is distance, and yous should choose meters every bit the advisable units of change.
How dissimilar exponential growth rates affect growth
The difference in the exponential growth rate r will have a significant influence on how quickly the observed quantity changes from the initial value. Let us start with 100 = 100 and, using the exponential growth calculator, see what x(10) will be for four different values of r:
| r | x0 | ten(x) |
|---|---|---|
| i% | 100 | 110.5 |
| 3% | 100 | 134.4 |
| 5% | 100 | 162.9 |
| 10% | 100 | 259.4 |
From this table, we see that all initial values are the same, being equal to 100 = 100, simply the final values of x(10) differ significantly. Your intuition may fox you hither considering the difference between 1% and 3% doesn't await similar much, only after x periods, this amounts to a 21.67% higher value for x(10) for iii%-growth as compared to ane%-growth.
If you lot compare the 10%-growth to 5%-growth, you will discover an even greater difference, 59.23% in favor of ten%-growth. You can find this contrast in the following graphical representation of the four exponential growth functions:
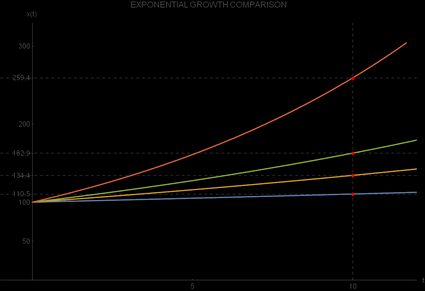
Comparison of exponential growths with different rates of growth
What are real-world applications of the exponential growth?
The formula for exponential growth and decay is used to model various real-world phenomena:
- population growth of bacteria, viruses, plants, animals and people
- decay of radioactive affair
- claret concentration of drugs
- atmospheric pressure of air at a sure height
- compound interest and economic growth
- radiocarbon dating
- processing ability of computers etc.
💡 And did yous know that...
you can verify if a set of numbers obeys the exponential growth formula past using the well-known Benford's law?
References
FAQ
How do I summate exponential growth?
Exponential growth is described by the formula:
Xₜ = Ten₀ × (one + r/100)ᵗ
where Xₜ is the quantity at fourth dimension t, X₀ is the initial value, r is the rate of change.
What is the difference betwixt exponential and linear growth?
Exponential growth occurs by multiplying the initial value past some constant factor at each time stride. Linear growth means we add the same corporeality at each time step.
How do I calculate exponential decay?
Exponential decay is given by the formula:
Xₜ = Ten₀ × exp(μt)
where Xₜ is the quantity at time t, 10₀ is the initial quantity, and μ is the decay constant.
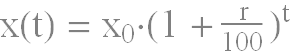
Source: https://www.omnicalculator.com/math/exponential-growth
Posted by: careydrife1958.blogspot.com

0 Response to "How To Find Initial Population With Exponential Growth"
Post a Comment